| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 밀레니엄 난제
- 곱의 미분
- 평균변화율
- 체인룰
- 모델 베유 군
- 합차의 미분
- 미분계수
- 4차원 도형
- 함수의 극한
- 미분
- 타원곡선 유리수점
- 유율법
- 초입방체
- 다항함수의 미분법
- 푸앵카레 정리
- 합성함수의 미분
- 도함수
- 버츠와 스위너톤 다이어 추측
- 실수배의 미분법
- 연쇄법칙
- 몫의 미분
- 하세 베유 l 함수
- 타원곡선
- 미분법
- 엡실론 n 논법
- 미분형식
- 미적분
- 수열의 극한
- 엡실론 델타 논법
- 극한
- Today
- Total
R수학연구소
[미적분] 2. 수열의 극한 (입실론-N논법) 본문
*저는 전문가가 아닙니다. 가볍게 이해하고 넘어가는 느낌으로 보시는 것을 추천합니다*
*틀린 부분이 있을 수 있습니다*
권장사항: 수열의 극한 (애매모호 Ver.) https://themathematics.tistory.com/7
애매한 정의
앞서 극한의 '한없이' 라는 표현이 애매모호하다고 했습니다. 그것이 극한의 핵심 개념인데 말이죠. 이에 수학자들이 이 문제를 해결하기 위해 극한을 재정의하기로 했다고도 했습니다.
코시와 한없음의 정의
바로 이때 등장한 수학자가 오귀스탱 루이 코시입니다. (코시-슈바르츠 부등식의 그 분 맞습니다.)

코시는 우선 '한없이'부터 정의해야 한다고 생각했습니다. 코시가 생각한 '한없이'는 다음과 같습니다.
1) 한도 $ \varepsilon $을 제시합니다.
2) 한도 $ \varepsilon $을 넘는 것을 찾습니다.
모든 $ \varepsilon $에 대하여 한도 $ \varepsilon $을 넘는 것이 있다면, 그것은 '한없다'라고 할 수 있다는 겁니다. 왜냐하면 그것이 한도가 있다면, 그 한도를 뛰어넘는 $ \varepsilon $이 있을 텐데 모든 $ \varepsilon $에 대하여 $ \varepsilon $을 넘는 것이 있다면 그건 불가능하기 때문입니다.
'그것' '넘다' 같은 포괄적인 언어 때문에 헷갈린다면, 아래 구체적인 예시를 봅시다.
ex1) $ f(x)=x $를 봅시다.
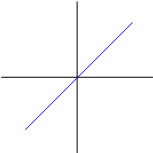
이 함수는 위로도, 아래로도 한없습니다.
어떤 $ \varepsilon $이 있다고 합시다. 그러면 한칸만 오른쪽으로 가면 $ \varepsilon $보다 큰 친구가 있습니다. 따라서 위로 한없습니다. 반대로 한칸만 왼쪽으로 가면 $ \varepsilon $보다 작은 친구가 있습니다. 그러니 아래로도 한없습니다.
하지만 이런 함수는 한도가 있습니다.
$ f(x)=x^2 $

위로는 한도가 없을 겁니다. 오른쪽으로, 또는 왼쪽으로 가면 항상 더 커지기 때문이죠.
그런데 아래로는 한도가 있습니다. $ \varepsilon = -1 $이라고 하면 $ f(x) $의 어떤 값도 -1보다 작아지지 않기 때문에 한도가 있습니다.
여튼 '한없음'이 정의되었으니 수렴을 정의할 차례입니다.
코시와 수렴의 정의
수렴은 정의가 쉽습니다. 수렴은 한없이 가까워지는 상태니 차가 한없이 작아지는 상태이기 때문이죠. (물론 양수이면서 한없이 작아지는 겁니다. 차는 아무리 작아봤자 0이니까요)
코시가 생각한 수렴의 정의는 다음과 같습니다.
1) 수렴한다고 예상되는 값 b를 찾습니다.
2) 수열 $ {a_n} $ 과 b의 차이를 구합니다.
3) 그 차가 한없이 작다는 것을 보입니다.
여하튼 코시는 이 내용을 수식으로 정리할 필요를 느꼈고, 이를 식으로 정리했습니다. 좀 지저분하다는 게 문제지만
$ \varepsilon>0 $인 $ \forall \varepsilon $에 대하여, n이 충분히 크면
$ \left| {a_n}-b \right| > \varepsilon $을 만족할 때, $ {a_n} $은 수렴한다.
$ \forall $은 전칭기호라고 하며, '모든'이라는 뜻을 가지고 있습니다. $ \forall \varepsilon $은 모든 $ \varepsilon $이라는 뜻이겠죠.
절댓값은 두려워할 필요가 없습니다. 양수니까 붙인 겁니다.
'n이 충분히 크면 $ \left| {a_n}-b \right| >\varepsilon $을 만족한다는 것은 차가 한없이 작다는 뜻이겠죠.
결국 다 합치면, 특정 값과 수열의 차가 양수이면서 한없이 작으면, 그러니까 한없이 가까워지면 수렴한다는 뜻입니다. 우리가 아는 수렴의 정의네요.
이와 같이 수렴을 엄밀하게 정의한 식을 $ \varepsilon - N $ 논법이라고 합니다.
'미적분' 카테고리의 다른 글
| [미적분] 6. 평균변화율 (0) | 2022.02.13 |
|---|---|
| [미적분] 5. 극한의 계산 (0) | 2022.02.07 |
| [미적분] 4. 함수의 연속 (0) | 2022.02.02 |
| [미적분] 3. 함수의 극한(엡실론-델타 논법) (0) | 2022.01.23 |
| [미적분] 1. 수열의 극한 (애매모호 Ver.) (0) | 2022.01.19 |




